Fonctions Sinus et Cosinus

Sinus et Cosinus

De la pesée du pain au sinus et au cosinus
On veut calculer sin ( A ) et/ou cos ( A ). On dispose d'une balance, d'un pain dont le poids est justement l'angle A et enfin d'une série de poids de valeur ArcTangente( 2^-j ). Dans la pesée, les poids ne peuvent aller que sur l'un ou l'autre des deux plateaux.

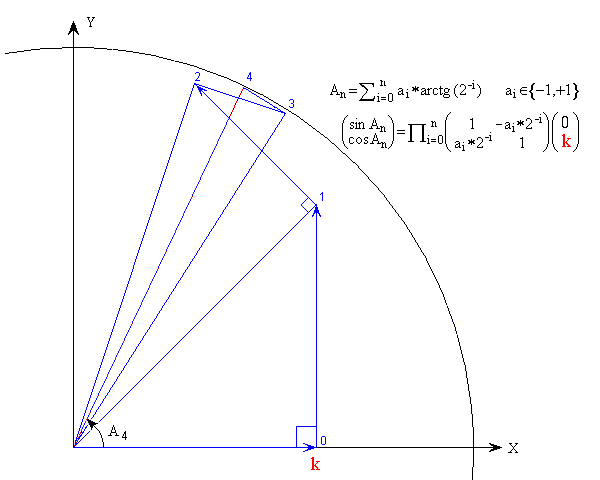
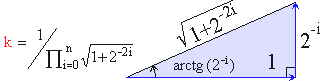
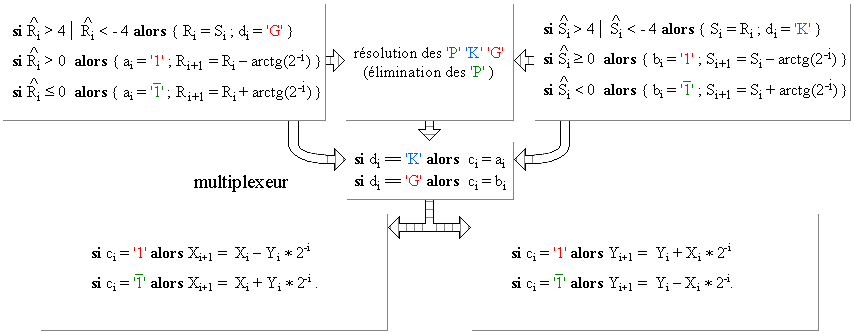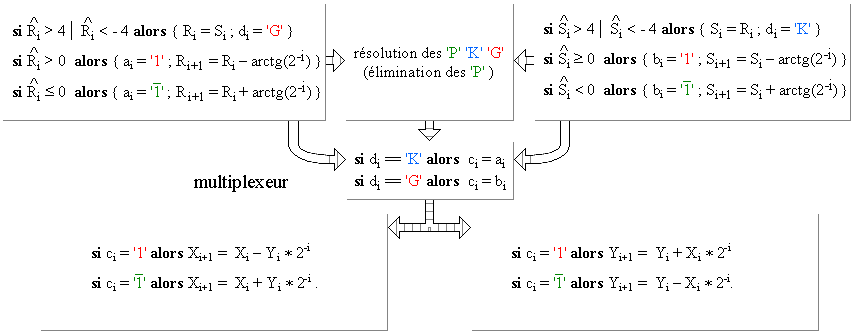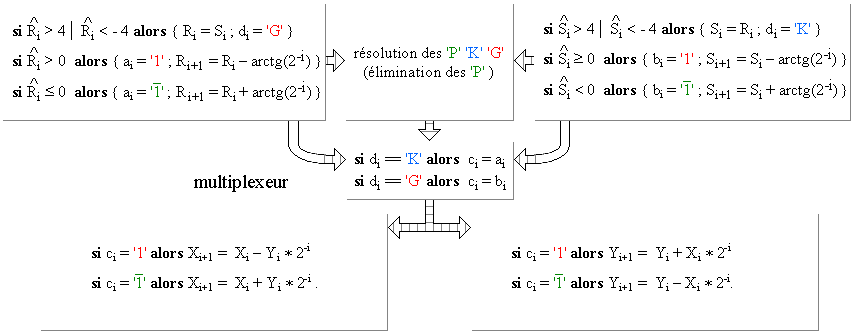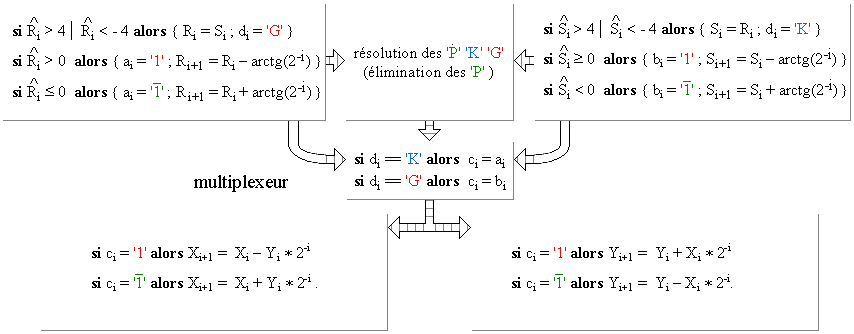
Calcul de Sinus et Cosinus

Soit un vecteur V_j d'extrémité (X_j, Y_j). Une "pseudoRotation" de V_j d'un angle arctg (2^-j) donne V_j+1 : X_j+1 = X_j – (Y_j * 2^-j) et Y_j+1 = Y_j + (X_j * 2^-j) . Une "pseudoRotation" de -arctg (2^-j) donne X_j+1 = X_j + (Y_j * 2^-j) et Y_j+1 = Y_j – (X_i * 2^-j). En décomposant un angle A en une somme de ± arctg (2^-j), une suite de "pseudoRotations" calcule les coordonnées du vecteur d'angle A et de module 1 qui sont les valeurs sin(A) et cos(A) cherchées. Pour chaque "pseudoRotations" on n'a effectué que une addition et une soustraction.

Décomposition d'un angle
Quel est le domaine des angles A = S _j a_j arctg (2^-j) et quelle précision espérer de cette écriture ? L'angle A est la valeur cherchée et l'angle T la valeur atteinte par la suite de "pseudoRotations". Cliquer dans la figure pour changer A. Les valeurs sont affichées en radian. La touche "Mise à zéro" laisse faire 'à la main' la conversion de A dans la base ± arctg (2^-j).

La constante k
Chaque "pseudoRotation" de ± arctg(2^-j ) entraîne un allongement du vecteur de Ö1+2^-2j, car elle n'est pas exactement une rotation mais un déplacement de l'extrémité du vecteur sur un vecteur perpendiculaire. Pour compenser par avance le produit des allongements d'une suite de "pseudoRotations", le vecteur de départ est ( X₀ = k , Y₀ = 0 ) . Pour n assez grand, k vaut environ 0,60725. Pour que k soit une constante, l'écriture dans la base arctg(2^-j ) utilise des chiffres a_j Î{ '-1' , '1' }.

"Diagramme de Robertson" pour sinus et cosinus

Le "diagramme de Robertson" montre que l'itération de conversion de l'angle dans la base arctg(2^-j ) peut être choisie comme suit:
si R ³ 0 alors { S = R – arctg(2^-j ) ; a_j = '1' } sinon { S = R + arctg(2^-j ) ; a_j = '-1' }.
Chaque itération est exécutée par un additionneur/soustracteur conditionnel.

Diviseur "sans restauration" pour sinus et cosinus
L'angle A en complément à 2 doit être dans l'intervalle [ -1, +1 [ . A = S _i v_i 2^-i (entrée en haut). Les bits de arctg(2^-j ) entrant dans les cellules "AS" sont câblés. Les opérations sont choisies par le signe des restes partiels R précédent et par v₀ pour la première opération .

Opérateur de "PseudoRotation" pour sinus et cosinus
Si les "PseudoRotations" utilisent des additions/soustractions sans propagation (ici en notation "CS") alors le délai est linéaire avec le nombre d'étages. Le premier étage n'effectue pas vraiment une addition, puisque X₀ = k , Y₀ = 0, en conséquence
si a₀ = '1' alors { X₁ = k ; Y₁ = k } sinon { X₁ = k ; Y₁ = - k }.
et pour les étages suivants ( j > 0)
si a_j = '1' alors {X_j+1= X_j– Y_j* 2^-j; Y_j+1= Y_j + X_j* 2^-j } // sens direct
sinon {X_j+1= X_j+ Y_j* 2^-j; Y_j+1= Y_j – X_j* 2^-j } // sens inverse
Pour clarifier le dessin, la nappe X_j * 2^-j ne figure pas toujours.

Cellule "RO"

La cellule "RO" est une variante de la cellule d'addition "CS" avec en plus une entrée "a_j" pour contrôler l'addition ou bien la soustraction. Observer que l'activité de la retenue entrante "e" ne se propage pas vers la retenue sortante "h".

si a_j = '-1' alors 2*co + s = eg + ed + ci // addition
si a_j = '1' alors 2*co + s = eg + 2 – ed + ci // soustraction

"Diagramme de Robertson" pour CORDIC à "double rotation"

Toutes les constantes arctg(2^-j) sont dans l'intervalle [ 0,7853982..  1 [ . Leur écriture en binaire commence donc toujours par "0,1". Elles sont donc normalisées et on peut utiliser un diviseur sans propagation qui détermine le sens de rotation avec uns approximation de l'angle résiduel R.
si > 0 alors a_j = '1' ; si = 0 alors a_j = '0' ; si < 0 alors a_j = '-1' .
On constate sur le diagramme que l'approximation peut être à ± 1/2 près.

Diviseur pour CORDIC à "double rotation"

Ce diviseur utilise les mêmes cellules "head" et "tail" que le diviseur "SRT". Pour s'accommoder du '0' (nécessaire) les "pseudoRotations" sont doublées. Grâce à cela l'allongement reste le même (1+2^-2j) pour les trois valeurs de a_j.

si a_j = '-1' alors { rotation de (-arctg(2^-j )) puis rotation de (-arctg(2^-j )) };
si a_j = '0' alors { rotation de (arctg(2^-j )) puis rotation de (-arctg(2^-j )) } ;
si a_j = '1' alors { rotation de (arctg(2^-j )) puis rotation de (arctg(2^-j )) } ;

Si l'angle A est dans l'intervalle [ -1,743..  +1,743...] la division ne déborde pas..

Diviseur pour CORDIC à "constantes réduites"
Si on multiplie toutes les constantes arctg(2^-j) par 3/4 on les ramène toutes dans l'intervalle [ 0,58904865..  0,75 [ et leur écriture commence maintenant par "0,10". Cette homothétie ne change pas la décomposition de l'angle V s'il est également multiplié par 3/4 en tirant partie des entrées positives et négatives du diviseur mais elle permet en revanche une cellule "head" bien plus simple donc plus rapide. Le reste est multiplié par 3/4.

"Double rotation" pour CORDIC
La constante k de la double rotation est le carré de la constante précédente. De plus la double rotation calcule sin(2*A) et cos(2*A). Il faut donc diviser l'ange A par 2 avant la division "SRT". .

Opérateur de double "PseudoRotation"
Pour chaque chiffre a_j on exécute successivement deux "pseudoRotations" d'angle arctg(2^-j) sans propagation de retenue.

La "double rotation" est coûteuse: elle double le matériel de la rotation et probablement le délai. En regroupant les lignes par deux elle se réécrit :

si a_j = '-1' alors
{ X_j+1 = X_j + 2 * Y_j * 2^-j – X_j * 2^-2j ; Y_j+1 = Y_j – 2 * X_j * 2^-j – Y_j * 2^-2j } ;
si a_j = '0' alors
{ X_j+1 = X_j + X_j * 2^-2j ; Y_j+1 = Y_j + Y_j * 2^-2j } ;
si a_j = '1' alors
{ X_j+1 = X_j – 2 * Y_j * 2^-j – X_j * 2^-2j ; Y_j+1 = Y_j + 2 * X_j * 2^-j – Y_j * 2^-2j} ;

Cette réécriture ne change pas le nombre d'addition/soustraction sauf lorsque les termes multiples de 2^-2j deviennent négligeables.
Peut on obtenir un résultat écrit avec des chiffres a_j Î{ '1', '-1' } (sans le '0' ) avec un délai comparable à celui du diviseur pour la double rotation? La conversion du quotient qui marche avec les poids 2^-j ( '0' '1' = '1' '-1' ) ne marche plus avec les poids arctg(2^-j ) .

CORDIC à "double division"
La "double division" est plus astucieuse que la "double rotation". Elle utilise deux des diviseurs précédents fonctionnant simultanément avec des cellules "head" légèrement modifiées.

"head" de diviseur1 (sortie a )
si > 0 alors { = – 2 ; a_j = '1' }
si £ 0 alors { = + 1 ; a_j = '-1' } "head" de diviseur2 (sortie b_j )
si ³ 0 alors { = – 2 ; b_j = '1' }
si < 0 alors { = + 1 ; b_j = '-1' }

Il est clair que lorsque = 0, le diviseur1 spécule que R £ 0 et diviseur2 que R ³ 0. L'un des deux au plus se trompe et en conséquence peut déborder. Le débordement se produira d'ailleurs avant l'apparition d'un autre = 0 dans l'un ou l'autre des diviseurs. Au débordement d'un diviseur on saura que le seul résultat correct est celui de l'autre diviseur.
Par commodité seul le diviseur1 est affiché par l'applet ci-dessous.

Les "head" des 2 diviseurs détectent leur débordement pour afficher ensemble un indicateur à 3 valeurs:
'K' le chiffre a_jde diviseur1 est correct (divisieur2 déborde), 'G' le chiffre b_jde diviseur2 est correct (diviseur1 déborde), 'P' propager l'indicateur suivant (pas de débordement, les deux chiffres a_j et b_j sont potentiellement corrects). Chaque fois qu'un diviseur déborde, il importe le reste partiel R de l'autre diviseur pour continuer. L'indication "Overflow" signale un débordement simultané et fatal de diviseur1 et de diviseur2.
L'élimination des 'P' est semblable à la propagation de retenue de l'addition et à la conversion du quotient.

Calcul de Tangente
Pour calculer la tangente d'un angle, on calcule sinus et cosinus puis on divise. Cependant la constante k n'intervient pas dans le quotient. On peut donc démarrer la rotation avec X₀ = 1 , Y₀ = 0, et simplifier en conséquence l'opérateur de "pseudoRotations" .