Additionneurs

Cellule "FA"

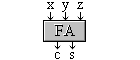
Dans la cellule "FA", la somme pondérée des bits en sortie est égale à la somme pondérée des bits en entrée c'est à dire que " x + y + z = 2*c + s ". Les trois bits en entrée ont le même poids, disons 1 pour fixer les idées, le bit sortant "s" a le même poids que "x", "y" et "z" et "c", un poids double (soit 2). La cellule "FA" conserve la valeur numérique comme en électronique les nœuds conservent le courant. La cellule "FA" est également appelée "réducteur 3 Þ2" car elle réduit le nombre de bits de 3 à 2 tout en conservant la valeur numérique.

Additionneur à propagation

L'addition est de très loin l'opération arithmétique la plus commune des processeur numériques. D'abord parce que l'addition en tant que telle est très fréquente, ensuite parce que l'addition est la base d'autres opérations arithmétiques comme la multiplication, la division, l'extraction de racines et les fonctions élémentaires. Tout assemblage "cohérent" de cellules "FA" conserve la propriété: la somme pondérée des bits qui sortent vaut la somme pondérée des bits qui entrent. Pour obtenir l'additionneur S = A + B, il faut que les bits entrant soient ceux des nombres A et B et les bits sortant forment le nombre S. Le nombre de cellules "FA" nécessaires pour additionner les deux entiers A et B est le nombre de bits de A et B.

Additionneur signé

La flèche verticale à côté du bouton de l'additionneur fait apparaître une double interprétation des vecteurs binaires A, B et S: entier sans signe (en haut) et entier signé dit en complément à 2 (en bas). Le même additionneur accepte ces deux interprétations à un détail près: le calcul du bit retenue sortante cn. On a le dilemme suivant: On ignore ce bit, on a un seul type d'additionneur et la somme S a autant de bits que les addendes A et B mais le débordement est possible. On tient compte de ce bit, pas de débordement possible mais l'additionneur d'entiers non signés est (légèrement) différent de l'additionneur d'entiers signés et S a un bit de plus que A et B. On préfère généralement la première solution. Une flèche verticale apparaît à côté de S et passe de l'une à l'autre écriture de S: n bits ou n+1 bits.

Performance de l'additionneur à propagation

Soit un additionneur à propagation à travers n cellules "FA", si on suppose que toutes les valeurs de A et B sont équiprobables et indépendantes, les résultats théoriques suivants viennent:   minimum moyen maximum délai 0 log2(n) n activité 0 3n / 4 n2 / 2 Le délai maximum (pire cas) n'est en général pas acceptable. Il est dû au chemin de la retenue qui traverse toutes les cellules "FA". Étudions donc le cheminement de la retenue.

Cheminement de la retenue

Pour la cellule "FA" de rang i, un des 3 cas se produit : la retenue ci+1 est mise à zéro, cas noté 'K', si ai = 0 et bi = 0 la retenue ci+1 est mise à un, cas noté 'G', si ai = 1 et bi = 1 la retenue ci+1 est propagée, cas noté 'P', si (ai = 0 et bi = 1) ou (ai = 1 et bi = 0). Dans ce cas ci+1 = ci. Ce dernier cas, défavorable pour le délai, est matérialisé par une flèche horizontale.

Ces trois cas 'K', 'G' et 'P' sont codées sur 2 bits. Une cellule "HA" calcule ces cas en fonction de ai et bi .

Cellule "BK" (Brent et Kung)

La cellule "BK" permet de calculer le cheminement de la retenue pour 2 cellules "FA" ou plus généralement pour 2 blocs de cellules "FA".

Additionneur de Sklansky

Pour concevoir un additionneur rapide, on va calculer toutes les retenues ci par des arbres binaires de cellules "BK". L'additionneur de Sklansky construit des arbres de retenue de 2 bits, 4 bits, 8 bits, 16 bits, 32 bits, ... en assemblant chaque fois 2 arbres de taille inférieure. L'architecture est simple et régulière, mais n'est pas toujours la plus économique en nombre de cellules.

Associativité et non commutativité

La cellule "BK" est associative comme on peut le verifier ci-contre, mais elle n'est pas commutative d'après sa table de vérité ( 'G' et 'K' ne permutent pas).

Additionneurs rapides (Brent et Kung)

Il y a une seule règle de construction des arbres imbriqués de cellules "BK": Toute retenue ci de rang i est reliée à toutes les entrées de rang j < i par un arbre binaire planaire de cellules "BK". Cela permet d'entrelacer les arbres des n sorties de très nombreuses façons en fonction du nombre de bit et du délai maximum de l'additionneur. Ce délai s'étend de (n-1) à log2(n), bornes comprises.

Dans les arbres de cellules "BK" on peut troquer des cellules "BK" contre du délai maximum: plus le calcul est rapide (moins de cellules "BK" à traverser), plus l'additionneur utilise de cellules "BK". faire varier le nombre de bits et/ou le délai. vérifier que les arbres suivent la règle de construction en cliquant sur un signal. remarquer que chaque signal a un nom unique composé de 2 chiffres. simuler un calcul de retenue en cliquant les touches . voir les détails de la construction des arbres avec la touche "Détails" voir la description en VHDL de l'additionneur avec la touche "VHDL". Pour récupérer la description VHDL dans un éditeur de texte, la copier puis coller. voir la table qui décrit ces arbres en cliquant la flèche verticale .

Additionneurs de Kogge et Stone

Les arbres binaire de cellules "BK" des additionneurs de Kogge et Stone ne partagent pas. En conséquence la sortance des signaux est réduite au minimum au prix de cellules "BK" plus nombreuses, et comme le délai dépend le la sortance, il est un peu plus court.

Additionneurs de Ling

Dans un additionneur de Ling, les arbres de "BK" calculent une primitive appelée "pseudo retenue". Ceci permet d'éviter le calcul des pi et gi, mais impose en revanche un calcul supplémentaire pour obtenir la retenue à partie de la "pseudo retenue". L'astuce est que le délai de ce calcul supplémentaire est recouvert par le délai des cellules "BK". En conséquence l'additionneur est plus rapide (un peu) que le "Kogge et Stone". La synthèse VHDL de l'applet précédent en tire partie si l'option "ling" est cochée.

Édition d'arbres de cellules "BK"

Pour éditer la table qui décrit les arbres de "BK", cliquer dans une case puis enter la valeur numérique de la case sélectionnée. Les valeurs incohérentes sont remplacées par 0, valeur indiquant "pas de cellule". La flèche verticale dévoile les arbres.

Ce système d'écriture des nombres entiers permet l'addition en un temps court et indépendant de la longueur des nombres. Cependant il utilise deux fois plus de bits que la notation standard. En conséquence une même valeur a plusieurs écritures (sauf 2k – 1). Parmi toutes les écritures, celle n'utilisant que des '0' et des '1' est unique. La flèche verticale à côté des nombres en change l'écriture sans en changer la valeur. La flèche verticale à côté du bouton bascule la présentation en chiffres "CS" ou bits.