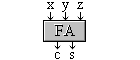
The "FA" cell conserves the sum just like the node conserves the electric current in the "Kirchoff's current law".
The "FA" cell is also called "3 Þ2 compressor" since it reduces the bits number from 3 to 2 while preserving the numerical value.
|
Adders |
|
|
In the "FA" cell, the weighted sum of the output bits equals the weighted sum of the output bits, i.e.
" x + y + z = 2*c + s ". The three input bits share the same weight. Let it be "1".
The output bit "s" has the same weight, while the output bit "c" weight is double (2). The "FA" cell conserves the sum just like the node conserves the electric current in the "Kirchoff's current law". The "FA" cell is also called "3 Þ2 compressor" since it reduces the bits number from 3 to 2 while preserving the numerical value. |
|
Carry propagate adder |
The addition is by far the most common arithmetic operation in digital processors. Addition is itself very frequent
and is also the basis of most other arithmetic operations like multiplication, division, square root extraction
and elementary functions. All "consistent" "FA" cells network preserves the property: the weighed sum of the output bits equals the weighted sum of the input bits. To construct the adder S = A + B, the input bits come from the two numbers A and B and the output bits form the number S. The number of "FA" cells is the number of bits of A and B. |
|
Signed adder |
The vertical arrow
The second solution is usually preferred. The vertical arrow |
|
Performance of the carry ripple adder |
Let us assume that all the possible values for A and B are equiprobable and independent:
|
|
Carry propagation path |
For each "FA" cell, one of the three following case happens :
|
| The three case 'K', 'G' and 'P' are encoded onto two 2 bits. Check the case above to show the 2 bits. A "HA" cell selects the case according to ai and bi. |
| The "BK" cell computes the carry for two binary positions ( two "FA" cells) or more generally two blocks of "FA" cells. |
| To design fast adders, binary trees of "BK" cells will first generate simultaneously all the carries ci. The "Sklansky's adder" builds recursively 2-bit adders, 4-bit adders, 8-bit adders, 16-bit adder and so on by abutting each time two smaller adders. The architecture is simple and regular, but suffers from fan-out problems. Besides in some cases it is possible to use less "BK" cells. |
|
Associativity and non commutativity |
The "BK" cell is associative as can be check on the applet at right, but its truth table shows clearly that is is not commutative ('G' and 'K' do not permutate). |
|
Fast adders |
In a fast adder, all the carries ci are computed simultaneously through a binary tree
of "BK" cells. To save on complexity, sharable intermediate results are computed once. There is only
one rule to construct the trees: every tree output with position i must be connected to all inputs
of position less than or equal to i by a planar binary tree of "BK" cells. The rule simplicity usually allows many correct constructions. |
|
In the "BK" cell tree, one may trade cells for delay, usually for the same addition the less the delay, the more "BK" cells needed.
|
| The binary trees of "BK" cells in the Kogge and Stone adders are not sharing. Consequently the signal fan-out is reduced to the minimum at the expense of more "BK" cells. Since the delay increases with the fan-out, it is now a bit shorter. |
|
Ling adder |
In the Ling's adder, the "BK" trees give a primitive called "pseudo carry". It avoids the computation of pi and gi, but on the other hand the carry has to be deducted from the "pseudo carry". The trick is that this late computation is overlapped by the "BK" cells delays. Consequently this adder is faster (a little bit) than the corresponding Kogge and Stone's adder. The VHDL synthesis from the applet takes advantage of Ling's approach if the box is checked. |
|
"BK" cell trees editor |
Check your understanding of Brent-Kung adder by creating new ones. Click on a position in the table to select it
and then enter a number with the keyboard. Inconsistent values are replaced by 0 (no cell). The arrow |
| In the "CS" cell, the weighted sum of the outputs equals the weighted sum of the inputs. In other words "a + b + c + d + e = 2*h + 2*g + f ". The "CS" cell is not only a "5Þ3 counter", but moreover the output "h" never depends on the input "e". |
| The "CS" cell does not propagate the input carry "e"
to the output "h". It makes "carry propagation free" adders possible. The number of necessary
"CS" cells is precisely given by the number of digits to be added. Nevertheless, each digit is coded onto 2 bits and the digit value is the sum of those 2 bits. Therefore the possible digit values are '0', '1' and '2' . |
| This notation system for integer numbers allows addition with a delay both short and independent
of the digits number. Yet this system demands about twice as many bits as the standard binary notation for a comparable
range. Consequently the same value may have several representations. Among the representations, the one with only
'0' or '1' is unique. The vertical arrow |
| We call "hybrid" the operators supporting different notations. The adder below, in some respects very simple, A is in binary, while B and S are both in "CS" notation. |