Time-Reversal PPM for Stress Wave Communications in Concrete Systems
Qing
Ji 1, Michael Ho 2, Rong Zheng 3, Zhi Ding 4 and Gangbing
Song 1,2
1.
Department of Electrical Engineering, University of Houston, Houston, TX, USA.
2.
Department of Mechanical
Engineering, University of Houston, Houston, TX, USA. Email: gsong@uh.edu
3. Department of Computing and Software, McMaster
University, Hamilton, ON, Canada.
4. Department
of Electrical Engineering, University of California, Davis, Davis, CA, USA.
ABSTRACT
Large concrete
structures are prone to cracks and damages over time from human usage,
weathers, and other environmental attacks such as flood, earthquakes, and
hurricanes. The health of the concrete structures should be monitored regularly
to ensure safety. A reliable method of real time communications can facilitate
more frequent structural health monitoring (SHM) updates from hard to reach
positions, enabling crack detections of embedded concrete structures as they
occur to avoid catastrophic failures. By implementing an unconventional mode of
communication that utilizes guided stress waves travelling along the concrete
structure itself, we may be able to free structural health monitoring from
costly (re-)installation of communication wires. In
stress-wave communications, piezoelectric transducers can act as actuators and
sensors to send and receive modulated signals carrying concrete status
information. The new generation of lead zirconate titanate (PZT) based smart aggregates cause multipath propagation in the homogeneous concrete channel, which presents
both an opportunity and a challenge for multiple sensors communication. We
propose a time reversal based pulse position modulation (TR-PPM) communication
for stress wave communication within the concrete structure to combat multipath
channel dispersion. Experimental
results demonstrate successful transmission and recovery of TR-PPM using stress
waves. Compared with PPM, we can achieve higher data rate and longer link distance via TR-PPM.
Furthermore, TR-PPM remains effective under low signal-to-noise ratio. This work
also lays the foundation for implementing multiple-input multiple-output (MIMO)
stress wave communication networks in concrete channels.
KEYWORDS
SHM,
stress wave communication, smart aggregate, time reversal, PPM, TR-PPM.
Introduction
Concrete
structures have been extensively used for over a century. However, in recent
years, many such structures have aged and deteriorated to the point of structural
failure, sometimes causing collapse-related accidents in many parts of the
world. The problem of aging infrastructure highlights the importance of
concrete structural health monitoring (SHM). With an increased focus on structural
integrity to meet safety regulations, there is an acute need for real-time
updates on health status of concrete structures, with continuous recording and
data export throughout the life cycle. Structural health monitoring (SHM)
related techniques provide an innovative potential to improve operational
safety of concrete structures while cutting down installation and maintenance
expenses. Recently, wireless sensor networks (WSNs) based
structure health monitoring have attracted increasing attention owing to their
low cost and ease of installation over conventional monitoring systems that
relying on piezoelectric sensors wired to a personal computer (PC), (e.g. Li et al. 2010). Although
optimized power system design and intelligent sleep management can increase the
lifetime of WSN SHM systems (e.g. Li et al. 2010), the need for battery replacement remains still a key
challenge for many civil applications (Hoult
et al. 2009). Furthermore, for structures buried underground or submerged
in water, it is difficult and often infeasible to use wireless RF communication.
Piezoelectric
based smart aggregate (SA) has proven to be effective both as sensors and
actuators, further enhacning its multi-functionality
in concrete SHM, including early age strength monitoring, impact detection and
structural health monitoring (Song et al.
2008). Additionally, smart aggregates can be employed for energy harvesting
from ambient vibration and long distance energy charging by focusing techniques.
For these reasons, it is natural and desirable to develop a fully autonomous
SHM system capable of damage detection, health monitoring, self
powering, and wire-free communication via the host concrete structure
itself as the channel medium.
Low
power, long range stress wave communication propagating
within the concrete structure is a very attractive solution. Thus far, works on
stress wave data communication in the structures are rather limited. Several
research teams have investigated ultrasonic digital communication through
metallic structures (e.g. Graham et al.
2009; Primerano 2010; Murphy 2006), though systematic
data communication schemes remain unclear. Kokossalakis
(2006) proposed using pipelines as an acoustic waveguide for modulated wave
transmission. Frequency-shift keying (FSK), amplitude-shift keying (ASK) and quadrature amplitude modulation (QAM) methods are shown to
have similar bit error performance. Several signal processing steps were
proposed to compensate for channel dispersion. Johnson (1972) tested seismic
communications with a data rate of two pulses per second at a distance of 760 ft
through hard rocks by using an impedance matched piezoelectric transducer as
the transmitter. Jin et al. (2011)
developed a time reversal based guided elastic wave communication scheme that
utilizes steel pipes as transmission channels for structural health monitoring
applications. Kailaswar et al. (2012) proposed a single-input single-output (SISO) communication paradigm using cement-based SA embedded
concrete channel based on the D8PSK modulation scheme. They observe that
multipath is not rich in concrete medium. Although the concrete medium is mostly
homogeneous, the new generation marble-based SA that consists of a piece of lead zirconate titanate
(PZT) patch sandwiched between a pair of
marble blocks through epoxy (Hou et al. 2012), contributing
to the inhomogeneous
channel environment for wave propagation. According to Snell’s law, as
the stress wave passes the border between media, the wave is reflected at the
interface and also refracted at an angle that depends upon the relative
refractive indices of the two media. Marble-based SAs
are more stable in mechanical performance compared with cement-based SAs. Hence, when applying marble-based SA for structure
health monitoring, a communication scheme is required to overcome the signal
delay spread caused by multipath channels. Furthermore, for future
consideration of multiple-input multiple-output (MIMO) communication links that
utilize stress waves propagating through concrete over the distances for
structural health monitoring, diversed multipath
dispersion across various transmit-receive paths can provide the useful MIMO
channel gain abd MIMO capacity. This channel diversity in MIMO system (e.g.
Sharony 2006) can take advantage of the dispersive
effects generated by inhomogeneous media for multiple-channel and simultaneous
multi-sensor transmission over the same concrete channel. With this
understanding, a communication scheme is needed to also overcome the resulting
multipath distortion when taking advantage of the multipath for MIMO
communications.
More
recently, there has been substantial interest in ultra-wide band (UWB)
communications because of its potentially low complexity and low power. Among
others, pulse position modulation (PPM) modulation offers notable advantage with
respect to power efficiency (Ramirez-Iniguez et al. 2008). In this paper, we develop a
novel method of PPM inside concrete using stress wave communications. To
mitigate distortions due to multipath channel dispersion, we propose a time
reversal based pulse position modulation (TR-PPM) for single channel (SISO)
stress wave transmission and reception. Our work contributes to the foundation
for future implementation of MIMO stress wave communications.
THEORETICAL BASICS AND DISCUSSION
a.
Channel Response and Stress Wave Propagation using different SAs
Two generations of SAs have
been developed for structural health monitoring. For the 1st
generation, the PZT patch
is embedded within a concrete block (Gu et al. 2006), whereas the 2nd
generation PZT patch is sandwiched between marble blocks. Piezoelectric materials can generate electric charge in response to
applied mechanic forces and can produce stress or strain when subjected to an
electric field. Under an alternating potential difference, the material is set
to elastic
vibration, which produces stress waves.
In
order to take full advantage of different SA properties for stress wave
communication in concrete blocks, it is necessary to characterize channel
response when different SAs are embedded into the
concrete specimen. Thus, two concrete cylinder specimens are set up as shown in
Figure 1. One cylinder is embedded with marble-based SAs
embedded while the other is embedded with cement-based SAs.
A 10mm thickness sponge sheet under the cylinders isolates wave propagation.
For each concrete cylinder, piezoelectric actuator and the piezoelectric
sensor, in the form of SAs, are positioned along the
central axis of the cylinder specimen, separated by a distance of 10 inches. In
the experiment, for both specimens, the actuator SA1 emits a sweep sine wave
and the sensor SA2 receives the stress wave from SA1. Figure 2 shows the spectrum
of the received signal by the sensors in two different specimens. The concrete
channel using marble-based SAs had better response in
high frequencies while the channel using cement-based SAs
had better response in low frequencies.

Figure 1.Two concrete cylinder specimens with different SAs
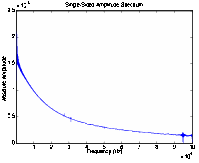
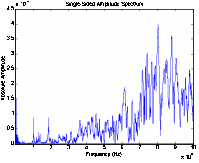
(a) Cement-based (b) Marble-based
Figure 2. Frequency response of two different
specimens
For
cylindrical concrete structures, stress waves can be generally categorized into
three families, namely the torsional (T),
longitudinal (L) and flexural (F) waves. There exist several different
guided wave modes in each family. Guided stress waves are known to be
dispersive because the wave mode velocity varies with its frequency. The
changes in phase velocity with respect to frequency are simulated for the concrete
used in the experiments (Figure 3) using software GUIGUW (Bocchini et al. 2011). While the fundamental
mode (L (0, 1), T (0, 1), F (0, 1)) is defined over the entire frequency range,
the branches of higher modes started to propagate at their cut-off frequency.
The cut-off frequencies of higher modes start from around 20 KHz. The number of wave modes increases as the frequency
increases. Higher frequency signals excite more propagation modes. The
fundamental torsional mode T (0, 1) is non-dispersive
while the other modes are highly dispersive, especially at their respective low
frequencies. In other words, a small change in frequency causes a relatively
large velocity change at low frequency. It is this non-constant channel group
delay that causes frequency dispersion. For each mode, as the frequency
increases, the level of dispersion decreases. In particular, a pulse may contain
a wide range of frequencies and potentially excites many modes
. Since the concrete channel using
cement-based SAs acts as a low pass filter, only the
fundamental modes are excited and the channel appears less dispersive. The
concrete channel using marble-based SAs has a good
high-frequency response, and the channel becomes more dispersive as more modes
are stimulated. As a result, a pulse signal traveling through the concrete becomes
heavily distorted when using the marble SAs. On one hand,
the multipath diversity may be potentially exploited by properly designed modulation
schemes in multi-antenna systems. On the other hand, the communication system
must also compensate for Inter-Symbol Interference (ISI) due to channel
dispersion.
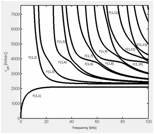
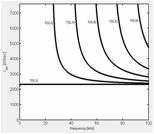
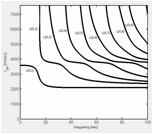
(a) Torsional modes
(b) Longitudinal modes
(c) Flexural modes
Figure 3. Phase speed
versus frequencies dispersion curves
b. Principle
of Time Reversal Communication
In order to combat severe channel dispersion, we
adopt time reversal communication utilizing the stress wave .
The spatial and temporal focusing property of time reversal can take advantage
of the dispersion caused by the channel by applying matched pulse-shape to
focus multipath energy for increasing received SNR. Time reversal technique has
been applied under dispersive channels in many applications, including defects
detection in pipes (e.g. Ying et al.
2010), underwater acoustics (e.g. Edelmann et al. 2005), electromagnetic (e.g. Jin et al. 2007), and stress wave communication, etc..
Consider an input signal x(t) generated by SA1. Let f(t) represent the
corresponding impulse response function, then, y(t) received by the SA2
can be written as
![]()
where![]() denotes
the convolution operation.
denotes
the convolution operation.
The
received signal at SA2 is reversed in time, namely time reversal signal y(-t),
![]()
When
the time reversed signal is sent from SA2 to SA1, assuming the channel is
reciprocal, the received signal can be given as
![]()
where![]() denotes time
correlation.
denotes time
correlation.
Most
of input signals are time reversal symmetric, such as Gaussian pulse,
sinusoidal signals, and square signals, i.e., x(-t)=x(t). Therefore, the received signal is a
convolution of input signal and an autocorrelation function
which is often called the time reversal operator. The operator named![]() , is represented as
, is represented as
![]()
From
Eq. (5), it is shown that the time reversal operator is an even function. Therefore
the received signal is always time reversal symmetric in the time domain. When t=0, time reversal operator has the
maximum value
![]()
This
proves that the received signal yTR(t) is a time
reversal symmetric focusing signal.
c. Design of PPM and TR-PPM
Communication

Figure 4. PPM and TR-PPM transmission
scheme
Figure 4 illustrates the basic diagram of
the (TR-)PPM transmitter in which the pulse-shaper can
executive TR-PPM by adopting the time-reversed waveform it received from its
partner node. This transmitter consists of the following components:
1.
The
binary source provides in binary format the information ![]() =
(
=
(![]() ,
,![]() ,
,![]() ,…,
,…,![]() ) that the stress wave needs to deliver.
) that the stress wave needs to deliver.
2.
Transmission
coder applies an integer-value code ![]() =
(
=
(![]() ,
,![]() ,
,![]() ,…,
,…,![]() ) to the binary sequence a
and generates a new sequence d
expressed as follows:
) to the binary sequence a
and generates a new sequence d
expressed as follows: ![]() , where
, where![]() is
the time hopping code which plays the role of code division multiple access for
multiple users, and
is
the time hopping code which plays the role of code division multiple access for
multiple users, and ![]() is the chip time.
is the chip time. ![]() represents the time shift
specified on the given chip block and
represents the time shift
specified on the given chip block and ![]() is
the symbol duration introduced by the PPM which depends on the bit to be
represented. In this paper, we used the basic PPM modulation scheme, that is
is
the symbol duration introduced by the PPM which depends on the bit to be
represented. In this paper, we used the basic PPM modulation scheme, that is![]() .
.
3.
PPM
Modulator generates a sequence of united pulses which
are located at times![]() .
.
4.
Pulse
shaper functions as a filter with impulse response![]() .
.
a. For the conventional PPM method, it can be the Gaussian modulated sine waveform
![]()
![]()
Where
![]() is the amplitude,
is the amplitude, ![]() is the normalized bandwidth,
is the normalized bandwidth, ![]() is the attenuation,
is the attenuation, ![]() is
the center frequency (Hz),
is
the center frequency (Hz), ![]() is the delay, and
is the delay, and ![]() is the samples.
is the samples.
b.
For
the TR-PPM method, ![]() where
where ![]() is
the channel impulse response,
is
the channel impulse response, ![]() is
the time reversed channel response waveform. The transmitting TR-PPM modulated
signal takes the form of
is
the time reversed channel response waveform. The transmitting TR-PPM modulated
signal takes the form of ![]()
EXPERIMENTAL SETUP
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Figure 5. Experimental setup
The
experimental setup (Figure 5) includes a concrete block of dimension 72”x5”x3”with
multiple marble-based SAs embedded inside. An network interface (NI) USB X Series 6361 Data Acquisition
System interfaced with a laptop through LabVIEW
software collects data, while a PZT amplifier boosts signal transmission. The
maximum input sampling rate of data acquisition system is 2 MHz per channel and
the input/output dynamic range is [-10V, 10V]. The data acquisition system
sent a signal through the analog output port to a PZT amplifier. The amplified
signal excites one of the SAs (as the
actuator) in concrete. The vibrating
signal propagated through the concrete, and is received by the other SA (as the
sensor). The analog input port of the data acquisition sensed the SA vibration
and acquired the received waveform for information extraction and decoding.
EXPERIMENTAL PROCEDURES
We
use the stress wave communication between SA2 and SA3 as an example to describe
the following steps in the experiments.
1.
Selection of a concrete channel resonance frequency as the center frequency for
modulated Gaussian pulse![]() : We use a sweep sine wave as the source signal to find
the suitable channel resonance frequency. Figure 6 shows a Gaussian modulated sinewave with 36 kHz center frequency.
: We use a sweep sine wave as the source signal to find
the suitable channel resonance frequency. Figure 6 shows a Gaussian modulated sinewave with 36 kHz center frequency.
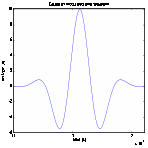
Figure 6. Gaussian modulated sine waveform
2. Transmission of a modulated Gaussian pilot signal is
sent, and measuring channel response between two SA:. Figure
7 shows received signal from SA3 when SA2 transmits a modulated Gaussian pulse at
center frequency of 36 KHz. The modulated Gaussian pulse waveform experiences
substantial dispersion after traveling through the concrete. This severe time
spreading response results from channel multipath and dispersion of stress
waves.
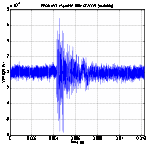
Figure 7. Channel response (SA2, SA3)
3. Reversal of normalized sounding signal and feedback: The channel sounding signal is time
reversed (Figure 8) and amplitude normalized (maximum amplitude value was scaled
to 500V), and then is retransmitted back to the same channel. The received signal
is a focused signal (Figure 9) with a distinct peak,
indicating that most energy from different wave modes arrive at the receiver
simultaneously. This peak allowed for accurate synchronization and signal
decoding when transmitting data streams. The reversed channel response waveform
is used to replace each pulse when modulating the data information in step
4.
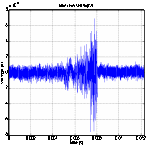
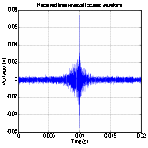
Figure 8. Time reversed signal (SA2, SA3) Figure 9. Received time reversal focused
waveform (SA2, SA3)
4. Transmission and
reception of modulated time reversal signals to the SA2 after encoding a stream
of binary bits. The binary streams were encoded through relative pulse shift
within each data frame based on the time reversed channel response signal. The
experiments are tested out at the data rates of 200 bps, 500 bps and 1 Kbps,
respectively. The maximum amplitude value of output waveforms from the analog
output port, which was the input of the amplifier, is scaled to the same value
at all times for fair comparison between PPM and TR-PPM communication methods.
EXPERIMENTAL RESULTS
Conventional PPM and TR-PPM communication experiments are
each carried out between different SA pairs under multiple transmission data
rates of 200 bps, 500 bps, and 1 Kbps. The following sub-sections compare the
results between the two different communication schemes under three
transmission data rates in three different scenarios: short range
communication, low signal-to-noise ratio (SNR) communication and relatively long distance
communication.
a.
Short Range Stress Wave Communication Experiments via PPM and TR-PPM
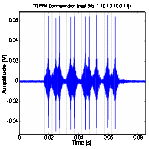
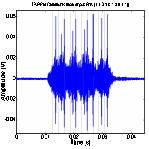
Figure 10 shows the experimental results at three
different data rates between the nearest SA pairs (SA2 and SA3) transmitting
the bit stream [1101010011]. The amplifier connected to the SA2 (as actuator)
outputs the excitation signal of peak amplitude value 500V. The received
information-bearing waveforms encoded by two different modulation communication
methods are compared. SA3 received the decodable waveforms for both PPM and TR-PPM at data rate
of 200 bps. For PPM communications, the received waveform becames harder to discern (or demodulate) at 500 bps and actually
fails to show signal peaks at 1 Kbps because of the severe signal dispersion.
However, TR-PPM communication results clearly show focusing peaks at both 500
bps and 1 Kbps data rates. We notice that there are several weak peaks at data
rates of 500 bps and 1 Kbps due to ISI. As the data transmission rate grows,
the ISI becames more significant. We conclud that transmitted stress wave signals can be decoded
better according to the clearly visible signals peaks in TR-PPM at higher data
transmission rate.
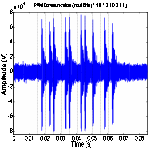
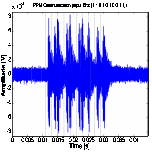
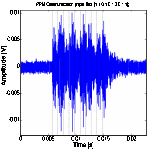
(a) PPM
at 200 bps data rate
(b) PPM at 500 bps data rate (c) PPM
at 1 Kbps data rate
(d) TR-PPM at 200 bps data
rate (e) TR-PPM at 500
bps data rate (f) TR-PPM at 1
Kbps data rate
Figure 10. PPM and TR- PPM communication between SA3
and SA4 with bit stream [1101010011].
b. Low SNR Stress Wave Communication
Experiments via PPM and TR-PPM
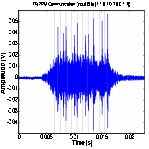
To
further evaluate the link performance at low SNR, we reduces
the maximum amplitude value of the modulated signal to 25V without changing the
main experimental settings (using SA2 and SA3). Similar to the previous
experiment, PPM and TR-PPM communication are tested and compared in three
different data rates (Figure 11). Comparing their received signals in Figure
10, it is clear that the SNR is lower given the reduced excitation signal. For
PPM, the received signal is fully submerged in noise and undetectable due to
the low SNR for all three data rates cases. But TR-PPM demonstrates robustness in low SNR conditions and
the advantage of energy focusing through time-reversal
pulse shaping. Although the peak values in Figure 11 are lower by roughly 10
times below those of Figure 10, the focused TR-PPM peaks still clearly convey
the transmitted binary data. Hence, TR-PPM method allows signal transmission at
substantially reduced SNR conditions.
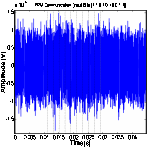
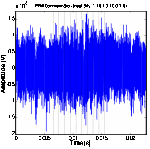
(a) PPM at 200 bps data rate (b) PPM at 500 bps data rate (c) PPM at 1 Kbps data rate
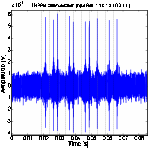
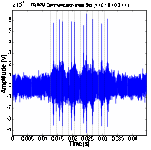
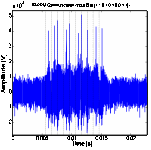
(d) TR-PPM at 200 bps data rate (e) TR-PPM at 500
bps data rate (f) TR-PPM at 1 Kbps data rate
Figure 11. PPM and TR- PPM communication between SA3 and SA4 in low SNR with bit stream [1101010011].
c. Long Distance Stress Wave Communication
Experiments via PPM and TR-PPM
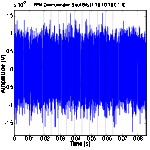
Figure
12 shows the received pulse focusing waveform and the received waveform at data
rates of 200 bps, 500 bps and 1 Kbps between the farthest SA pairs (i.e., SA1
and SA5). The maximum amplitude of excitation signal is 500 V. Compared with
Figure 9, the focused peaks between SA1 and SA5 become wider than those between
SA2 and SA3. This is because of the substantial signal attenuation at longer
distance that weakened multipath signal strength, since time reversal
techniques achieve signal focusing by using energy from all paths, Also, background
noise becomes relatively stronger to degrade the received signal energy quality
due to the weaker signal strength through longer distance.
We
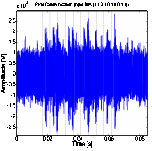
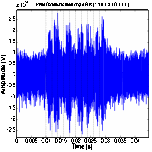
find the received PPM signal peaks become difficult to detection under all
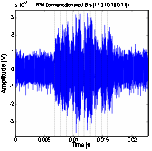
three different transmission rates. For TR-PPM, the peaks clearly convey the stream of binary
data at 200 bps. When the transmission
data rate increases to 500 bps or 1 kbps, the peaks starts to widen and overlap
and became less distinguishable because of the relatively longer channel delay
spread versus the modulated pulse interval. Although it is expected for achievable
transmission rate to drop as transmission distance groups, TR-PPM maintains its
performance edge over the traditional PPM.
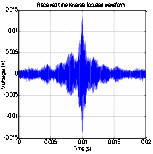
(a) Received time reversal focused waveform (SA1, SA5)
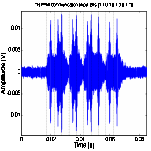
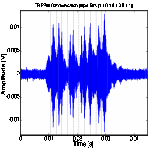
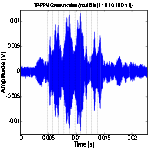
(b) PPM at 200 bps data rate (c) PPM at 500 bps data rate (d) PPM at 1 Kbps data rate
(e) TR-PPM at 200 bps data
rate
(f) TR-PPM at 500 bps data rate (g) TR-PPM at 1 Kbps data
rate
Figure 12. PPM and TR- PPM communication between SA1
and SA5 with bit stream [1101010011].
Conclusions
In
this paper, we studied Marble-based SA pairs as actuator and sensor for
transmitting and receiving encoded binary data information over concrete
channels. We show that the received stress wave signal encounters severe channel
dispersion when using conventional PPM and often becomes difficulty to detect. We
introduce a time reversal technique for PPM (TR-PPM) that can focus pulsed
waves through inhomogeneous multipath channels by utilizing the scattering of
waves. Compared with PPM communication, TR-PPM substantially improves data
rate, transmission distance, and is robust at lower SNR environment. This work further provides a foundation
for future implementation of MIMO stress wave communication links in concrete
channels.
ACKNOWLEDGMENTS
The authors are grateful to Dr. Peng
Li for assisting with SA integrated system testing, analysis
of the concrete communication channel, and also for providing suggestions and
expertise on conducting the communication experiments in concrete. This
material is based upon work supported by NSF awards (CNS-0832089 and
CCSS-CPS1102195).
References
Li, P., Gu, H., Song, G., Zheng, R. and Mo, Y.L. (2010). “Concrete structural health monitoring using piezoceramic-based wireless sensor networks. Smart Structures
and Systems, 6(5-6), 731-748.
Li, P., Olmi, C. and Song, G. (2010). “Energy efficient
wireless sensor network for
structural health monitoring using distributed embedded piezoelectric transducers”, In [SPIE Smart Structures and Materials+
Nondestructive Evaluation
and Health Monitoring], International Society for
Optics and Photonics,
764715-764715.
Hoult, N.A., Fidler, P.R.A. and Middleton,
C.R. (2009). “Wireless Structural Health Monitoring of Bridges: Current Challenges and Future Innovations”, Proceedings of the 7th AustRoads Bridge Conference, 1-12.
Song, G., Gu, H. and Mo, Y.L. (2008). “Smart aggregates:
multi-functional sensors for concrete
structures—a tutorial
and a review”, Smart
Materials and Structures, 17
(3), 1-17.
Graham, D., Neasham, J., and Sharif, B. (2009). “High bit rate
communication through
metallic structures using electromagnetic acoustic
transducers", OCEANS 2009-EUROPE,
1-6.
Primerano, R. A.
(2010). “High Bit-rate
Digital Communication through
Metal Channels", Doctoral
thesis, Drexel University.
Murphy, T. (2006). “Ultrasonic
Digital Communication System for a Steel Wall Multipath Channel: Methods and Results", Master's thesis, Rensselaer Polytechnic Institute.
Kokossalakis, G.
(2006). “Acoustic Data Communication
System for In-pipe wireless
sensor network”, PhD thesis, Massachusetts Institute
of Technology, Cambridge, MA.
Johnson,
C. C. (1972). “A seismic communications investigation
employing a piezoelectric transducer”.
Jin, Y., Zhao, D., and Ying, Y. (2011).
“Time reversal data communications on pipes using
guided elastic waves - Part I: Basic principles”, in [SPIE
Smart Structures/NDE Conference],
1-12.
Jin,
Y., Ying, Y., and Zhao, D. (2011). “Time reversal data communications on pipes
using guided elastic waves - Part II: Experimental studies”, in [SPIE Smart Structures/NDE Conference],
1-11.
Kailaswar,
S., Zheng, R., Kovitz, J., Phung Q.,Wang
H., Ding Z. and Song, G. (2012). “ConcreteCom: A New
Communication Paradigm for Building Structural Health Monitoring”, in Proceedings of the Fourth ACM Workshop on
Embedded Sensing Systems for Energy-Efficiency in Buildings, 131-137.
Hou
S., Zhang H.B., and Ou J.P. (2012) “A PZT-based smart
aggregate for compressive seismic stress monitoring”, Smart Materials and Structures, 21(10), 105035, 1-9.
Sharony,
J. (2006). “Introduction to Wireless MIMO–Theory and
Applications”, CEWIT–Center of Excellence in Wireless and Informational
Technology, Stony Brook University, IEEE LI, 1-63.
Ramirez-Iniguez, R., Idrus, S. M., and
Sun, Z. (2008). “Optical wireless communications: IR for
wireless connectivity”, Boca Raton: CRC Press.
Gu,
H., Song G., Dhonde H., Mo Y.L., and Yan S. (2006). “Concrete
early-age strength monitoring using embedded piezoelectric transducers”, Smart Materials and Structures, 15(6),
1837-1845.
Bocchini
P., Marzani A., and Viola E. (2011). “Graphical user interface for guided acoustic waves”, Journal of Computing in Civil Engineering,
25(3), 202-210.
Ying,
Y., Soibelman, L., Garrett, J., Jin, Y., Moura, J., Oppenheim, I., O’Donoughue,
N., and Harley, J.
(2010). “Time reversal detection in pipes”, in [SPIE Conference on Smart Structures/NDT], 7647, 76473S-1-12.
Edelmann, G., Song, H., Kim
S., Hodgkiss, W., Kuperman,
W., and Akal, T. (2005). “Underwater acoustic communication using
time reversal”, IEEE J. Ocean. Eng., 30(4), 852-864.
Jin,
Y., Jiang, Y., and Moura, J. M. F. (2007). “Multiple antenna time reversal transmission in ultra-wideband
communications”, in [IEEE Globe
Communication Conference], 3029-3033.